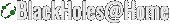https://blackholesathome.net/ wrote:April 2021 Update
TL;DR: Tremendous progress has been made, and BlackHoles@Home is on target for an August 2021 launch!
Here is a technical update showing some of our latest results. Please refer to sections below this one for a more basic introduction to the project.
BlackHoles@Home is a proposed BOINC project that aims to fit binary black hole simulations on consumer-grade desktop computers. In doing so we can enlist the general public to help generate the large gravitational waveform catalogs that form the foundation for a great deal of gravitational wave science.
Traditionally, these binary black hole simulations have been performed on supercomputers. BlackHoles@Home implements new approaches for robustly solving Einstein's equations of general relativity in highly efficient coordinate systems, so that these simulations will fit on consumer-grade desktop computers in only a few gigabytes of RAM.
In particular BlackHoles@Home makes use of the following numerical grid structure:
- BHatHgrids.png (335.95 KiB) Viewed 2905 times
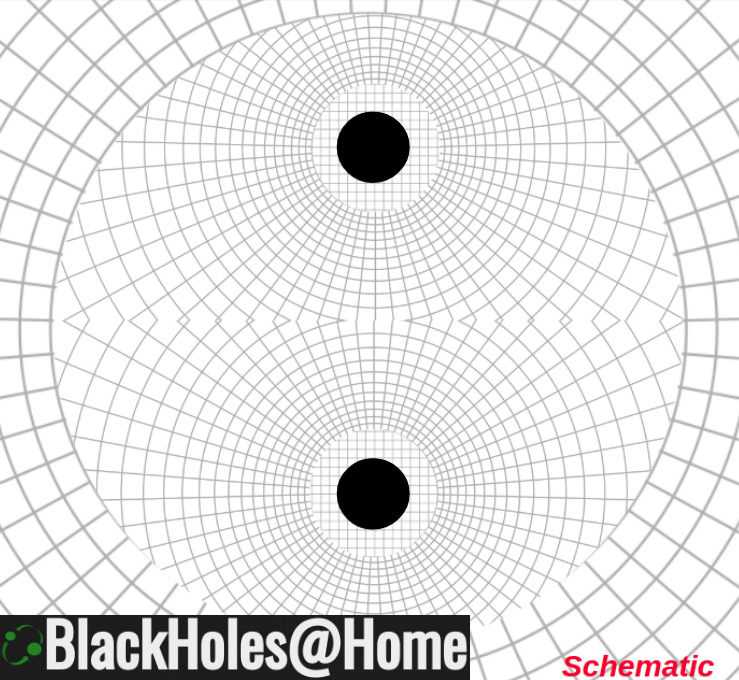
Compare this to the most popular approach for solving Einstein's equations, which does not exploit near-symmetries in the problem, instead opting for equally robust nested Cartesian grids at varying resolutions ([url =
https://en.wikipedia.org/wiki/Adaptive_mesh_refinement]adaptive mesh refinement[/url]):
- CartesianAMR.png (584.69 KiB) Viewed 2905 times
We performed a simulation of
the first black hole collision ever observed by gravitational wave detectors, which contributed to the
2017 Nobel Prize in Physics. The simulation was performed both using a trusted code (the Einstein Toolkit, which uses adaptive mesh refinement), and BlackHoles@Home. This happens to be an
Einstein Toolkit gallery example, which provides an interesting and very well documented example of the Toolkit's capabilities. Also the ET simulation results are
publicly available on Zenodo.
Basic initial properties of this binary black hole system:
10M initial separation
q=36/29=1.24 mass ratio
0.31 = spin component of more massive black hole (direction parallel to the orbital angular momentum vector)
-0.46 = spin component of less massive black hole (direction parallel to the orbital angular momentum vector)
Numerical details:
Both codes solve Einstein's equations using the BSSN formalism
Both codes compute partial derivatives with finite differences at 8th order accuracy
The ET simulation enables Kreiss-Oliger dissipation at 9th order, spatially constant with strength parameter set to 0.1.
BlackHoles@Home enables Kreiss-Oliger dissipation at 9th order, spatially varying such that it is effectively disabled inside the black holes and maximized in the weak-field region.
The ET numerical grids are as follows:
Strong-field region: Cartesian AMR grids, courtesy the Carpet code.
Weak-field region: Cubed sphere grids, courtesy the Llama code
Highest resolution of the Cartesian grids (near the black holes) is around M/52.
The outer boundary of the ET domain is 2200M.
BlackHoles@Home grids are as follows:
Strong-field region: Each black hole is housed within a small SinhCartesian AMR grid patch with one level of refinement; surrounded by a SinhSpherical grid. The SinhSpherical grids overlap.
The gravitational wavezone adopts a single SinhSpherical grid.
Highest resolution of the SinhCartesian grids (near the black holes) is around M/80.
The outer boundary of the BlackHoles@Home domain is 768M.
Note that the BlackHoles@Home simulations are ongoing (running between 6.2 and 8.5 M/hr), and several of the following plots will be updated. The BlackHoles@Home simulations in the following few plots use only 1.78GB of RAM, where the Einstein Toolkit uses 98GB.
The payload of the simulation is a gravitational wave prediction. As is standard, we decompose the gravitational wave content into s=2 spin-weighted spherical harmonics for efficiency. The dominant (l=m=2) mode of gravitational waves (real part of psi_4; the second time derivative of gravitational-wave strain, extracted at r=100M in the ET and 108M in BlackHoles@Home) agrees extremely well with the trusted code:
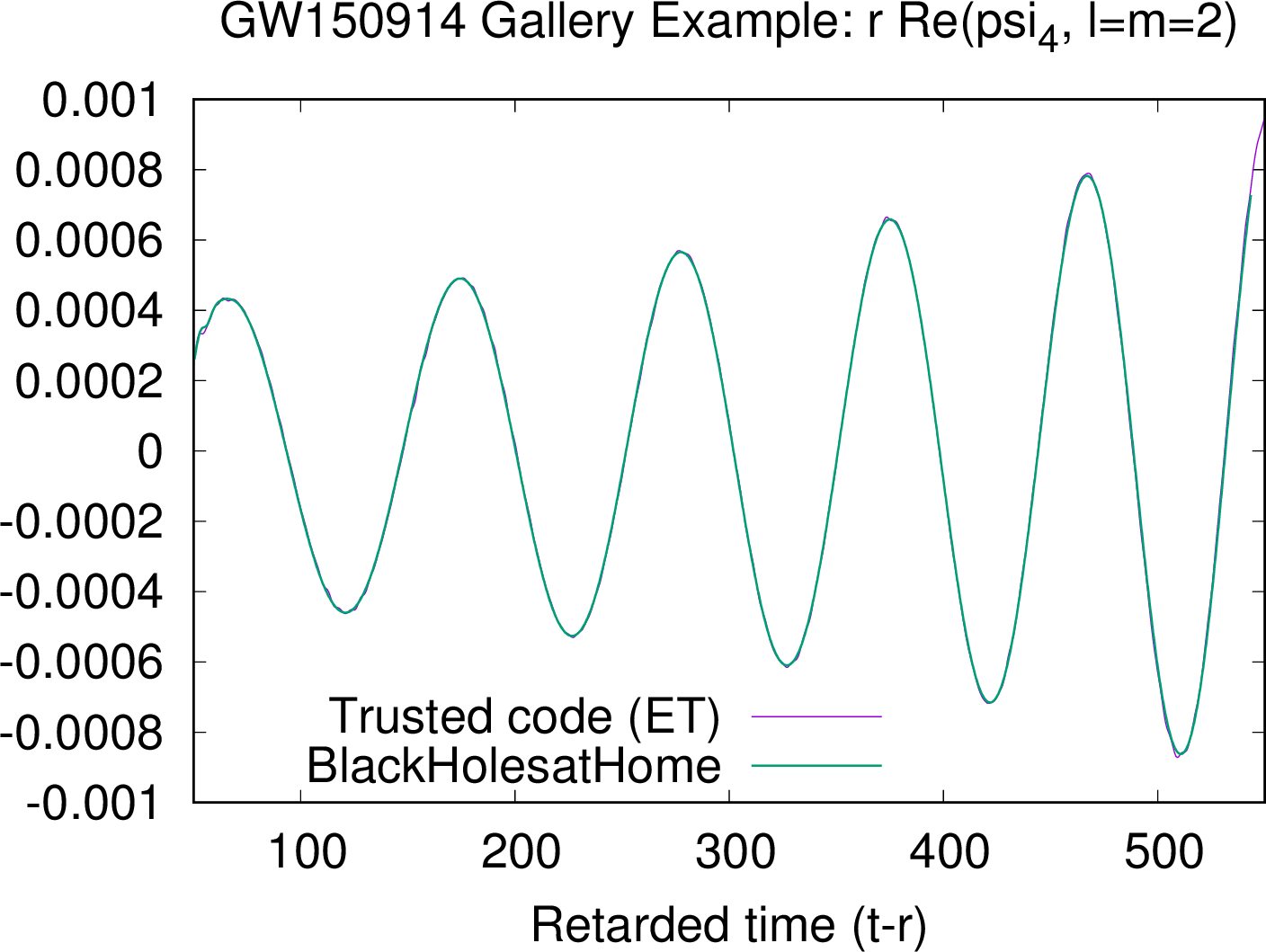
- psi4_l2m2.png (161.18 KiB) Viewed 2905 times
Excitingly the dominant higher-order (l=m=4) mode of gravitational waves is not as noisy in BlackHoles@Home, as compared to the ET!
This noise stems from numerical errors as high-frequency waves reflect off of adaptive mesh refinement boundaries in space and time (see this paper, and this paper). The number of grid boundaries is minimized in the BlackHoles@Home grids, and as a result the numerical noise is much less.
Next we show a measure of logarithmic numerical error (log10 absolute value of Hamiltonian constraint violation) on the orbital plane, after about 1.5 orbits of the binary black hole. The largest errors exist inside the black holes, thus the black holes appear as yellow dots.
First the result from the Einstein Toolkit (a trusted code), using 98GB of RAM:
Next from BlackHoles@Home, using only 1.78GB of RAM:
Notice the numerical errors are significantly smaller almost everywhere in BlackHoles@Home, as compared to the ET!
Upon further analysis we find the numerical errors are dominated by the small number of gridpoints sampling the polar angle in the small spherical grids surrounding each black hole. When this number is increased from 48 to 56, the errors drop significantly, and the memory usage increases only slightly to 1.83GB:
Increasing this to 64, the errors drop further (memory usage increases to 1.89GB):
Newsletter
Want to know what's on the horizon?
Sign up for the BlackHoles@Home newsletter
Basic Introduction
Slides from the BlackHoles@Home APS 2019 press conference
People
Zachariah B. Etienne is an associate professor of Physics & Astronomy at West Virginia University. Ian Ruchlin was a postdoctoral fellow at West Virginia University.